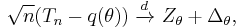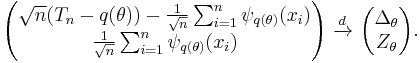Hájek–Le Cam convolution theorem

In statistics, the Hájek–Le Cam convolution theorem states that any regular estimator in a parametric model is asymptotically equivalent to a sum of two independent random variables, one of which is normal with asymptotic variance equal to the inverse of Fisher information, and the other having arbitrary distribution.

The obvious corollary from this theorem is that the “best” among regular estimators are those with the second component identically equal to zero. Such estimators are called efficient and are known to always exist for regular parametric models.

The theorem is named after Jaroslav Hájek and Lucien Le Cam.

Theorem statement

Let ℘ = {P_θ | θ ∈ Θ ⊂ ℝ^k} be a regular parametric model, and q(θ): Θ → ℝ^m be a parameter in this model (typically a parameter is just one of the components of vector θ). Assume that function q is differentiable on Θ, with the m × k matrix of derivatives denotes as q̇_θ. Define

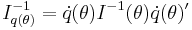$I_{q(\theta)}^{-1} = \dot{q}(\theta)I^{-1}(\theta)\dot{q}(\theta)'$ — the information bound for q,

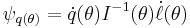$\psi_{q(\theta)} = \dot{q}(\theta)I^{-1}(\theta)\dot\ell(\theta)$ — the efficient influence function for q,

where I(θ) is the Fisher information matrix for model ℘, 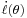$\scriptstyle\dot\ell(\theta)$ is the score function, and ′ denotes matrix transpose.

Theorem (Bickel 1998, Th.2.3.1). Suppose T_n is a uniformly (locally) regular estimator of the parameter q. Then

There exist independent random m-vectors 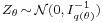$\scriptstyle Z_\theta\,\sim\,\mathcal{N}(0,\,I^{-1}_{q(\theta)})$ and Δ_θ such that

$\sqrt{n}(T_n - q(\theta)) \ \xrightarrow{d}\ Z_\theta %2B \Delta_\theta,$

where ^d denotes convergence in distribution. More specifically,

$\begin{pmatrix} \sqrt{n}(T_n - q(\theta)) - \tfrac{1}{\sqrt{n}} \sum_{i=1}^n \psi_{q(\theta)}(x_i) \\ \tfrac{1}{\sqrt{n}} \sum_{i=1}^n \psi_{q(\theta)}(x_i) \end{pmatrix} \ \xrightarrow{d}\ \begin{pmatrix} \Delta_\theta \\ Z_\theta \end{pmatrix}.$
If the map θ → q̇_θ is continuous, then the convergence in (A) holds uniformly on compact subsets of Θ. Moreover, in that case Δ_θ = 0 for all θ if and only if T_n is uniformly (locally) asymptotically linear with influence function ψ_q(θ)

References

Bickel, Peter J.; Klaassen, Chris A.J.; Ritov, Ya’acov; Wellner Jon A. (1998). Efficient and adaptive estimation for semiparametric models. New York: Springer. ISBN 0-387-98473-9.